Bonjour à tous ! Voici un tutoriel qui présente l’interpolation de Lagrange et les équations paramétrées. Combinées, ces deux techniques pourraient être un bon moyen de permettre à un robot d’effectuer une trajectoire courbe. C’est parti !
Introduction
L’un des objectifs pour un robot en termes de déplacement est de pouvoir effectuer des trajectoires courbes au lieu d’une succession de segments. Ce tutoriel propose une méthode pour créer un système de courbes paramétrées définies à partir des positions par lesquelles on souhaite que le robot passe.
Ce tutoriel sera en 3 parties : l’interpolation avec de la théorie et un exemple simple, les équations paramétrées, et une application de ces deux outils pour la trajectoire d’un robot.
Objectifs du tutoriel
- PARTIE 01 : Savoir interpoler plusieurs points dans le plan avec un polynôme
- PARTIE 02 : Comprendre ce qu’est une courbe paramétrée et quelles sont les propriétés intéressantes pour trouver une courbe complexe
- PARTIE 03 : Construire une trajectoire de robot
PARTIE 01 : L’interpolation
L’interpolation est définie ici comme une méthode pour trouver une ligne qui relie différents points prédéfinis. L’interpolation la plus simple est la ligne brisée, avec la constructions de droites entre deux points successifs. Mais puisque l’objectif est que le robot effectue une trajectoire courbe, une autre forme d’interpolation sera préférée : l’interpolation de Lagrange.
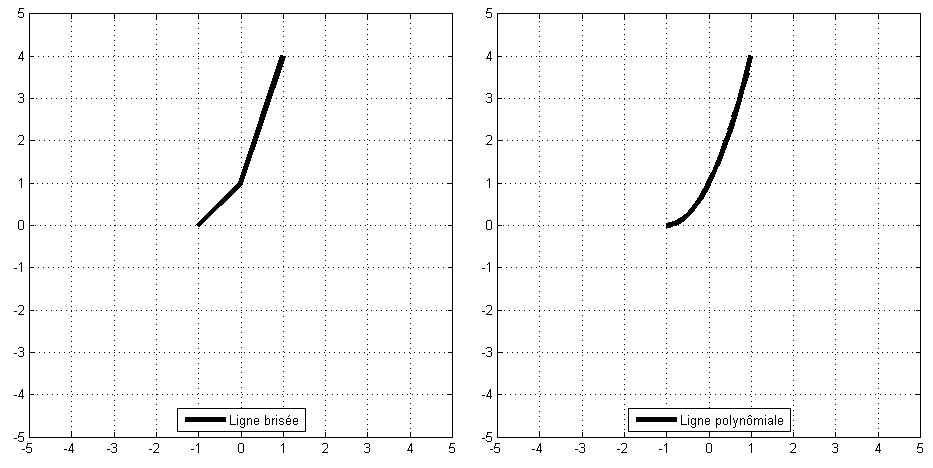
Différences entre une trajectoire formée à partir de droites et une trajectoire obtenue par interpolation de Lagrange.
Les deux courbes passent par les points (-1,0), (0,1) et (1,4), mais elles n’y passent pas de la même manière.
Les données d’entrée et la sortie souhaitée
Pour faire une interpolation, il faut des coordonnées de points dans le plan. L’interpolation renvoie en sortie le polynôme qui passe par ces points.
La formule
Pour ceux qui veulent des formules, voici la clé de tout le tutoriel !
L(X) = \sum _{j=0} ^{n} y_j \left ( \prod _{i=0, i \ne j} ^{n} \dfrac{(X-x_i))}{(x_j - x_i)} \right )
Le raisonnement en coulisses.
La formule ainsi est bien simple, mais il est préférable de la comprendre avant de l’appliquer. Il faut voir l’interpolation de Lagrange comme une somme de sous-polynômes qui s’annulent en tous les points sauf 1, et ce pour chaque point. Puis, il suffira d’ajouter ces polynômes pour former un super-polynôme qui répondra aux attentes.
Un exemple avec 3 points
Supposons que le polynôme recherché doive passer par les points \left\{ ({\color{Red} {-1}},{\color{Green} 0});({\color{Blue} 0},{\color{Magenta} 1});({\color{Purple} 1},{\color{DarkOrange} 4}) \right \}.
Dans un premier temps, seuls les abscisses des points sont considérées. Les ordonnées seront traitées dans un second temps. Pour cela, il faut trouver 3 polynômes qui vérifient les conditions suivantes :
- Le premier polynôme doit s’annuler en
{\color{Blue} 0}et en{\color{Purple} 1} - Le second doit s’annuler en
{\color{Red} {-1}}et en{\color{Purple} 1} - Le dernier doit s’annuler en
{\color{Red} {-1}}et en{\color{Blue} 0}
Pourquoi cela ? Parce que la deuxième étape de l’interpolation consiste à faire une combinaison linéaire de ces sous-polynômes. Si on arrive à contrôler à quel endroit lesquels s’annulent, la combinaison linéaire sera plus simple.
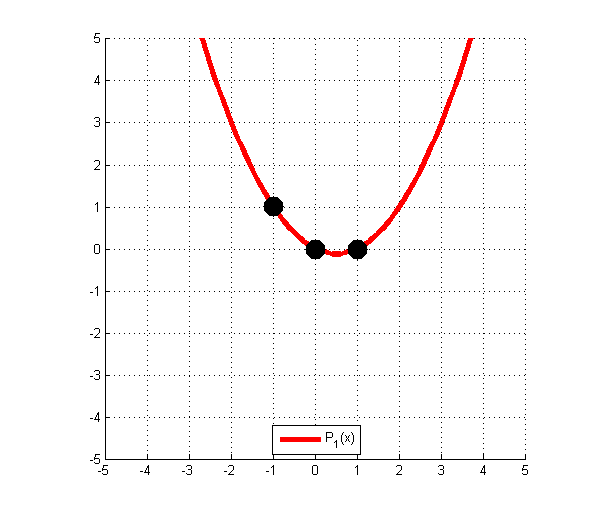
Le premier polynôme se trouve ainsi :
P_1 (x) = \dfrac{(x-{\color{Blue} 0}) \times (x-{\color{Purple} 1}))}{({\color{Red} {-1}}-{\color{Blue} 0}) \times ({\color{Red} {-1}} -{\color{Purple} 1})} = \dfrac{x^2 -x }{2}
Il s’agit bien du polynôme qui s’annule en 0 et en 1. De plus, ce polynôme vaut 1 en {\color{Red} {-1}}. Ce n’est pas tout à fait ce qui est recherché, mais ce n’est pas important pour le moment. Le voici en image :
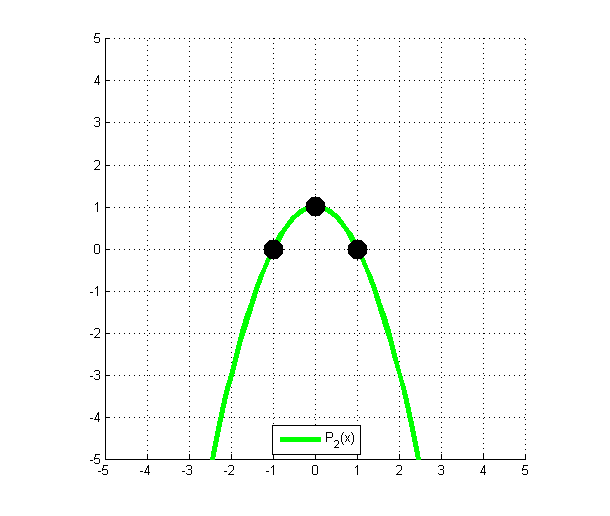
Le second polynôme se trouve ainsi :
P_2 (x) = \dfrac{(x-({\color{Red} {-1}})) \times (x-{\color{Purple} 1}))}{({\color{Blue} 0}-({\color{Red} {-1}})) \times ({\color{Blue} 0}-{\color{Purple} 1})} = 1-x^2
Il s’agit bien du polynôme qui s’annule en -1 et en 1. De plus, il faut 1 en {\color{Blue} 0}.
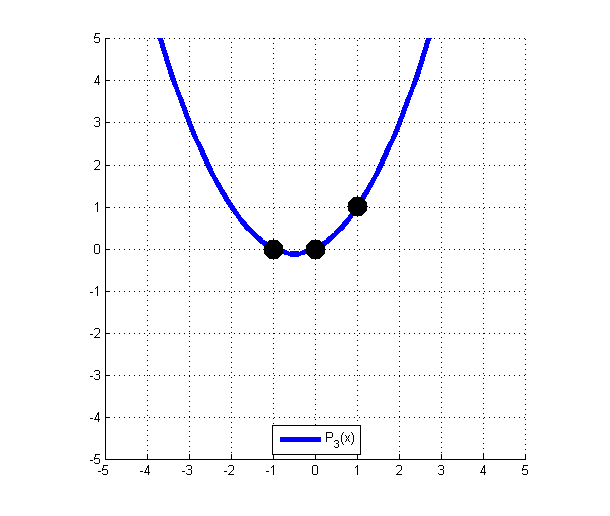
Le dernier polynôme se trouve ainsi :
P_3 (x) = \dfrac{(x-({\color{Red} {-1}})) \times (x-{\color{Blue} 0}))}{({\color{Purple} 1}-({\color{Red} {-1}})) \times ({\color{Purple} 1}-{\color{Blue} 0}))} = \dfrac{x^2+x}{2}
Il s’agit bien du polynôme qui s’annule en -1 et en 0. De plus, il vaut 1 en {\color{Purple} 1}.
Après s’être occupé des abscisses, place aux ordonnées ! Comme dit plus haut, les ordonnées se trouvent en faisant des combinaisons linéaires entre les sous-polynômes. La manière la plus simple de les combiner serait de les additionner. Voyons ce que ça donne :
P(x) = \dfrac{x^2 -x }{2} + 1-x^2 + \dfrac{x^2+x}{2} = 1
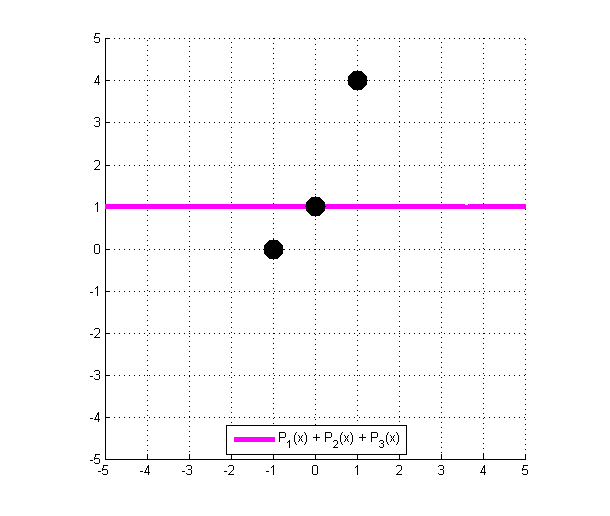
Dans le cas présent, en additionnant les trois polynômes, on trouve le polynôme constant égal à 1. Même s’il passe PAR HASARD par le point (0,1), il ne passe pas par les autres.
C’est pas encore ça. En effet, P({\color{Red} {-1}}) = 1 \ne {\color{Green} 0} , et P({\color{Purple} 1}) = 1 \ne {\color{DarkOrange} 4} .
Avant de trouver le super-polynôme, il faut garder une idée à l’esprit. En regardant les 3 sous-polynômes au point {\color{Red} {-1}}, il est possible de constater qu’ils valent TOUS 0 SAUF P_1 . Cette remarque est importante car elle signifie que quelque soit la combinaison linéaire, SEUL P_1 (et la constante qui le multiplie) impose sa loi pour la valeur en {\color{Red} {-1}}. De même, c’est P_2 qui impose sa loi pour la valeur en {\color{Blue} 0}. Et en {\color{Purple} 1}, c’est P_3 qui pilote. Du coup, l’enjeu de trouver les constantes nécessaires pour retrouver {\color{Green} 0}, {\color{Magenta} 1} et {\color{DarkOrange} 4}.
Pour cela, il suffit simplement de multiplier chaque sous-polynôme par le résultat qu’on attend de lui.
P(x) = {{\color{Green} 0}} \times {\dfrac{x^2 -x }{2}} + {{\color{Magenta} 1}} \times \left ( {1-x^2}\right ) + {{\color{DarkOrange} 4}} \times {\dfrac{x^2+x}{2}} = x^2 + 2x +1
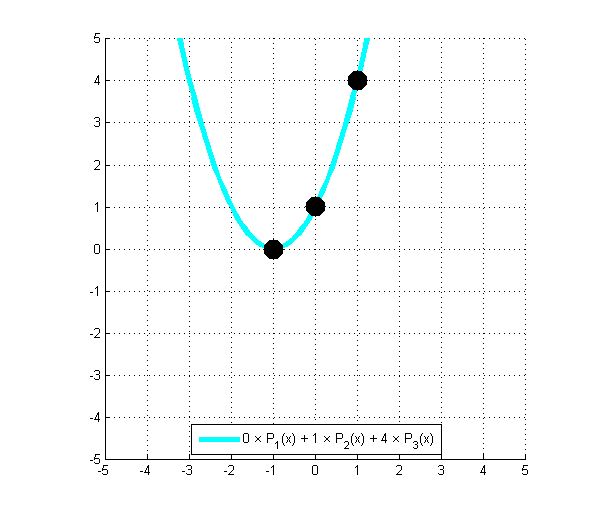
Les lecteurs les plus avertis remarqueront qu’il s’agit du polynôme {\left ( x+1 \right ) }^2 qui a été reformé à partir des trois points de départ.
Résumé de la partie théorique
- L’interpolation de Lagrange permet de relier des points du plan entre eux grâce à un polynôme.
- Pour cela, il faut calculer des « sous-polynômes » qui s’annulent pour toutes les abscisses sauf une, et ce pour chaque point.
- Ensuite, il faut multiplier chaque sous-polynôme par l’ordonnée attendue.
- Puis, le « super-polynôme » est formé en additionnant ces « sous-polynômes ».
PARTIE 02 : Les courbes paramétrées
Introduction
La plupart du temps, les équations qui sont manipulées sont de la forme y = f(x). f représente une fonction dont l’équation lie x et y. Mais ce n’est pas le seul type d’équation qui existe. L’autre grand type d’équation concerne les équations paramétrées, qui sont définies de la manière suivante : \left \{ \begin{matrix} x(t) = f(t) \\ y(t) = g(t) \end{matrix} \right. où f et g sont deux fonctions dépendant d’un paramètre t.
Attention, t n’a pas nécessairement de lien avec le temps. Il s’agit juste d’un paramètre qui sert à définir séparément x et y. Cependant, dans certains cas, il exprime en effet le temps, comme dans certaines équations en physique par exemple.
Remarque : Dans certains cas, il est possible de passer d’une équation paramétrée à une équation classique de la forme y = f(x). Par exemple : \left \{ \begin{matrix} x(t) = 4 \times t \\ y(t) = e^{t/2} \end{matrix} \right. \Leftrightarrow y = e^{x/8}Mais ce sont des cas particuliers. Généralement, et c’est l’un de leurs avantages, il n’existe pas de lien direct entre les deux termes d’une équation paramétrée.
Une particularité intéressante
Les courbes paramétrées ont également une propriété très intéressante : Puisque les variations de x et de y sont uniquement liées à celles de t, il est possible d’obtenir des courbes qui associent plusieurs valeurs de x pour la même valeur de x. Par exemple : \left \{ \begin{matrix} x(t) = t^2 \\ y(t) = t+4 \end{matrix} \right. \Leftrightarrow \left \{ \begin{matrix} (1,3) \ pour \ t = -1 \\ (1,5) \ pour \ t = 1 \end{matrix} \right.
Cette propriété a permis de définir de manière paramétrique les ellipses, et en particulier les cercles. La figure qui suit montre une ellipse centrée en (-1,1), dont le demi-axe sur X vaut 3.5 et le demi-axe sur y vaut 2.5. Le paramétrage associé à cette équation est donc le suivant :
\left \{ \begin{matrix} x(t) = -1 + 3.5 \times cos(t) \\ y(t) = 1 + 2.5 \times sin(t) \end{matrix} \right. \ pour \ t \in \left [ 0,2\pi \right ]
La représentation de l’ellipse est donc comme ceci :
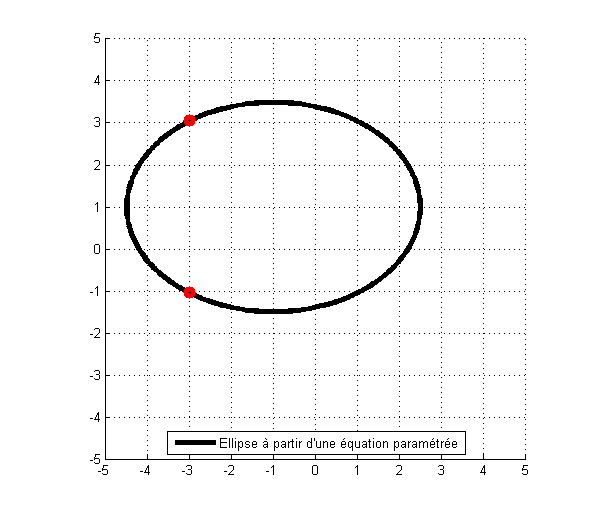
Ici, on voit bien que pour le point d’abscisse -3, il existe deux ordonnées, l’une en -1 et l’autre en 3. Ce cas ne serait pas possible avec une équation classique, mais il est possible grâce aux équations paramétrées.
Et les ellipses ne sont qu’un cas particulier des courbes paramétrées ! En cherchant sur Internet, on constate que plein de personnes créatives ont su utiliser les courbes paramétrées pour faire plein de choses, même des portraits ! Voici celui de Tupac, imaginez la longueur des termes de l’équation paramétrée !
Conclusion
Cette partie a été assez courte, l’idée centrale qu’il faut comprendre est que les courbes paramétrées sont un autre moyen de définir une courbe. L’un de leurs avantages principaux est de pouvoir faire des courbes qui à une même abscisse associent plusieurs ordonnées, ce qui permet d’obtenir des courbes plus complexes.
PARTIE 03 : On mélange tout ! La trajectoire d’un robot
Introduction
Les deux ingrédients principaux nécessaires au calcul de la trajectoire d’un robot sont maintenant en place ! Puisqu’il y a eu beaucoup de théorie pour le moment, voici un cas concret d’application.
Situation de départ
Supposons que le robot doive passer par les points suivants : \left \{ (0,2.5);(-1,1.5);(0,0);(3,0) \right \}. La situation est la suivante :
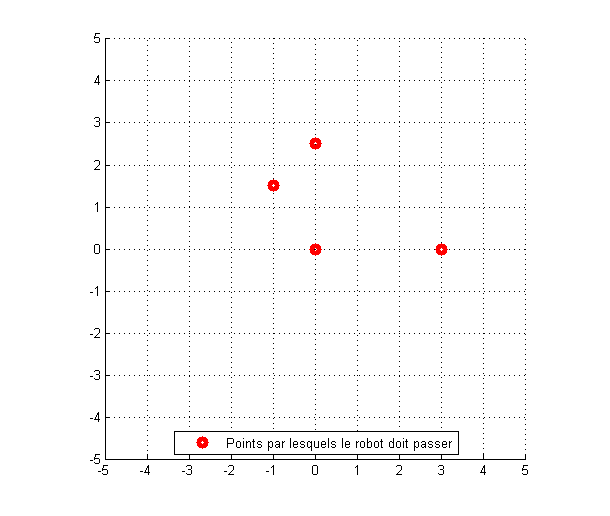
Votre mission si vous l’acceptez :
Trouver la trajectoire du robot pour qu’il passe par ces 4 points.
La solution la plus simple est bien-sûr de tracer une lignes brisées entre les points pour obtenir la trajectoire. D’accord, mais ce tutoriel a pour but de générer des trajectoires courbes ! Comment faire ?
Facile ! On a 4 couples de points, on peut utiliser l’interpolation !
Mmh, pas tout à fait. En regardant bien, la trajectoire fait passer le robot par deux points dont l’abscisse est la même mais dont l’ordonnée est différente : (0,2.5) et (0,0). Comment faire dans ce cas ?
Facile ! On décale légèrement l’un des points ! Le robot passera par (-0.001,0) au lieu de (0,0) !
Pas bête ! C’est vrai que le but est de trouver une équation pour un robot. Et un léger décalage des points à atteindre ne se verra pas lors du déplacement réel du robot. Mais cette solution ne marche pas. Je vous épargne les calculs, mais voici la solution que l’on trouverai avec l’interpolation :
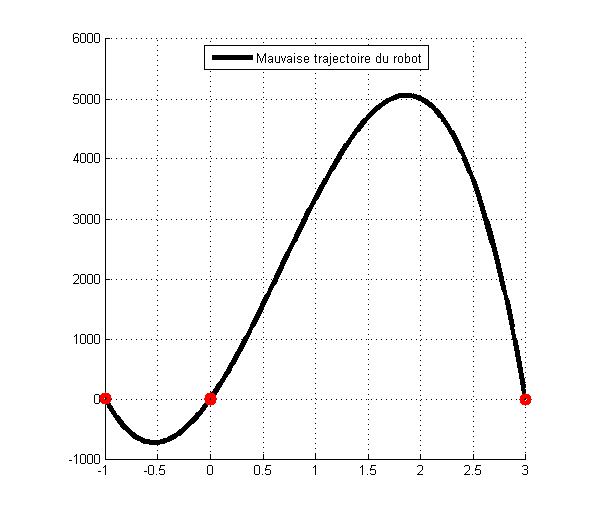
Regardez l’échelle des ordonnées, elle n’a plus aucun sens !
On croirait même que les points (0,2.5) et (-0.001,0) sont confondus !
Pour les personnes intéressées, voici l’équation : y(x) = -\dfrac{277 \ 625x^3}{333}+\dfrac{4 \ 440 \ 779 x^2}{2 \ 664}+\dfrac{2 \ 221 \ 481 x}{888}+\dfrac{5}{2}.
Le léger décalage a en effet permis de construire un polynôme qui passe par les 4 points. Mais ici, on veut que le robot passe par \left \{ (0,2.5);(-1,1.5);(0,0);(3,0) \right \} et dans cet ordre !
Du coup on peut pas le faire !
Bien-sûr que si, il faut juste comprendre qu’on ne peut pas le faire de la manière classique. Pour mieux comprendre, il faut avoir un autre regard sur ce que doit faire le robot. Voici un tableau pour expliquer ça :
| Ordre de passage | Coordonnée x | Coordonnée y |
|---|---|---|
| 1 | 0 | 2.5 |
| 2 | -1 | 1.5 |
| 3 | 0 | 0 |
| 4 | 3 | 0 |
Ce tableau montre quelque chose d’important : l’ordre de passage. On retrouve cette notion d’ordre de passage dans les équations paramétrées, avec le fameux paramètre t. La clé pour résoudre ce problème est alors la suivante :
Il faut créer deux équations paramétrées, une pour x et une pour y, qui dépendent chacune de l’ordre de passage. Dès lors, il faut résoudre cette partie en deux temps : D’abord pour x, puis pour y.
Cas de x
Pour bien comprendre, il faut imaginer que l’on cherche à interpoler les couples de points suivants : \left \{(1,0);(2,-1);(3,0);(4,3)\right \}. Cette courbe n’a pas vraiment de sens réel, si ce n’est qu’elle correspond juste à l’évolution du déplacement selon l’axe X. Puisqu’il y a 4 points, il faut construire 4 sous-polynômes sur le même principe qu’en partie 01 :
P_1 (t) = \dfrac{(t-2) \times (t-3) \times (t-4)}{(1-2) \times (1-3) \times (1-4)} = -{\dfrac{(t-2) \times (t-3) \times (t-4)}{6}}P_2 (t) = \dfrac{(t-1) \times (t-3) \times (t-4)}{(2-1) \times (2-3) \times (2-4)} = \dfrac{(t-1) \times (t-3) \times (t-4)}{2}P_3 (t) = \dfrac{(t-1) \times (t-2) \times (t-4)}{(3-1) \times (3-2) \times (3-4)} = -{\dfrac{(t-1) \times (t-2) \times (t-4)}{2}}P_4 (t) = \dfrac{(t-1) \times (t-2) \times (t-3)}{(4-1) \times (4-2) \times (4-3)} = \dfrac{(t-1) \times (t-2) \times (t-3)}{6}
Comme expliqué précédemment, il faut combiner ces polynômes ensemble pour obtenir :
x(t) = \left [ 0 \times P_1 (t) \right ] + \left [ (-1) \times P_2 (t) \right ] + \left [ 0 \times P_3 (t) \right ] + \left [ 3 \times P_4 (t) \right ] = t^2 - 4t + 3
Cas de y
Pour y, il faut construire 4 sous-polynômes. Mais avant de partir bille en tête, il faut bien comprendre ce qu’on fait ! Les sous-polynômes sont construits à partir des « abscisses » des points que l’on veut interpoler (donc l’ordre de passage). Ici, on interpole x en fonction de t et y en fonction de t. Donc dans les deux cas, les abscisses sont calculées à partir des valeurs de t ! Donc dans les deux cas, les sous-polynômes sont les mêmes ! Inutile de les recalculer, il suffit simplement de changer la combinaison linéaire ! Cela donne :
y(t) = \left[ 2.5 \times P_1 (t) \right] + \left[ 1.5 \times P_2 (t) \right] + \left[ 0 \times P_3 (t) \right] + \left[ 0 \times P_4 (t) \right] = \dfrac{t^3}{3} - \dfrac{9t^2}{4} + \dfrac{41t}{12} +1
Expression de la trajectoire finale
L’équation
L’expression de y est un peu plus complexe, mais elle est correcte ! Le système final s’écrit donc :
\left \{ \begin{matrix} x(t) = t^2 - 4t + 3 \\ y(t) = \dfrac{t^3}{3} - \dfrac{9t^2}{4} + \dfrac{41t}{12} +1 \end{matrix} \right.
La solution en image
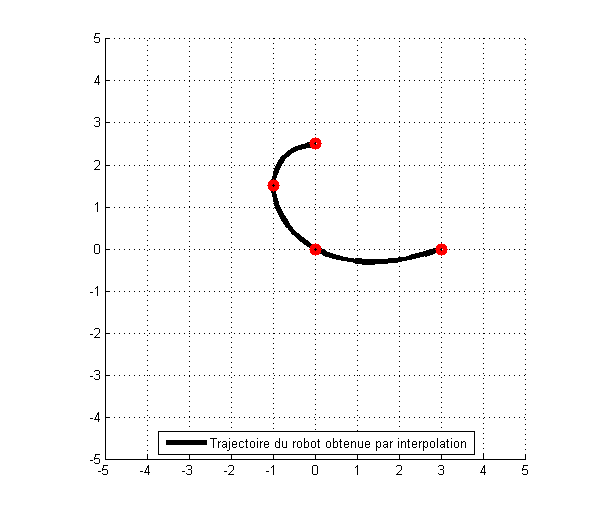
La trajectoire passe bien par les 4 points imposés. Grâce aux courbes paramétrées qui permettent d’interpoler x et y séparément, on peut obtenir une courbe qui « revient sur elle-même » en quelque sorte.
Conclusion de la partie pratique : Comment trouver la trajectoire d’un robot ?
- Définir les points par lesquels le robot doit passer ainsi que l’ordre de passage
- Calculer les sous-polynômes à partir de l’ordre de passage
- Calculer le super-polynôme associé à x en faisant une combinaison linéaire de ces sous-polynômes avec les valeurs de x
- Avec les mêmes sous-polynômes, calculer le super-polynôme associé à y en faisant une combinaison linéaire de ces sous-polynômes avec les valeurs de y
- Le système d’équations paramétrées ainsi obtenu définit la trajectoire du robot.
Conclusion générale et perspectives
Ce tutoriel était assez dense car il combine des aspects différents des mathématiques, mais il était important de bien définir les notions pour comprendre comment implémenter la solution. Concernant l’implémentation d’ailleurs, celle-ci est assez simple lorsqu’il y a peu de points. Elle est un peu plus lourde lorsqu’il faut plus de points, mais elle reste théoriquement valable.
Pour les personnes intéressées, un tableur Excel est disponible en cliquant ici. Il montre un exemple pour interpoler les points de ce tutoriel, mais chacun peut entrer les points qu’il veut. Les formules implémentées correspondent à celles du tutoriel. Par ici pour le télécharger !
L’interpolation de la Lagrange n’est pas la seule manière de relier des points par une courbe. Une autre forme d’interpolation qui fonctionne sur un principe similaire est l’interpolation trigonométrique, dont l’explication est sur Wikipedia par exemple. D’autres méthodes permettent aussi de trouver une courbe qui passe par des points voulus avec une valeur de tangente en ces points définie par l’utilisateur. Ces méthodes sont très intéressantes et lorsqu’on réfléchit à une trajectoire de robot, il est important de choisir la méthode qui convient le mieux.
N’hésitez pas à faire remonter les questions que vous pourriez avoir ! À bientôt !

Merci, je cherchais ce type d’explication depuis longtemps. C’est très clair.